Paquetes necesarios
library(tidyverse)
library(agricolae)
library(multcomp)
library(lsmeans)
library(multcompView)
library(ggpubr)
library(knitr)Diseño completamente al azar
Ejemplo
Se realizó un experimento en el cultivo del plátano fruta (Musa AAAB), clon FHIA 01v1 utilizando un diseño completamente al azar con el objetivo de evaluar 3 frecuencias de riego. Los tratamientos fueron los siguientes:
- T1: Regar diariamente (7riegos).
- T2: Regar interdiario (3,5 riegos)
- T3: Regar cada 3 días (2 riegos semanales).
Se probó cada frecuencia en un campo de una unidad rotacional en un sistema de riego localizado. En cada campo se muestrearon 20 plantas.
Para evaluar los tratamientos se utilizó como variable:
El peso de racimo en Kg
Datos
Una vez importada esta tabla de datos R, se debe transformar a forma Tidy donde cada variable debe ser una columna, para este caso tratamientos y peso, esto se hará a traves de la función gather
Transformacion de datos a foma Tidy
A traves de la funcion as_factor, transformamos la variable tratamientos a un factor de tres niveles.
datos_tidy <- datos %>% gather(key=tratamientos, value= peso)
datos_tidy$tratamientos <- as_factor(datos_tidy$tratamientos)
str(datos_tidy)## tibble [60 x 2] (S3: tbl_df/tbl/data.frame)
## $ tratamientos: Factor w/ 3 levels "trat1","trat2 ",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ peso : num [1:60] 35.5 36.1 38.3 33.7 39.2 42.3 45.1 36.7 35.1 36.9 ...Crear modelo
Para esto usamos la funcion aov donde evaluamos la variable peso en funcion de los tratamientos.
modelo<-aov(peso~tratamientos,data=datos_tidy)
summary(modelo)## Df Sum Sq Mean Sq F value Pr(>F)
## tratamientos 2 1743.2 871.6 65.29 1.8e-15 ***
## Residuals 57 760.9 13.3
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Como se observa en los resultados el Fvalue es mayor que la Ftab por lo que podemos concluir diciendo que existen diferencias significativas entre los tratamientos (***), pero no sabemos entre cuales por lo que debemos aplicar una prueba de comparación de medias.
Prueba de Duncan
duncan <- duncan.test(modelo,"tratamientos",alpha=0.05, console = TRUE)##
## Study: modelo ~ "tratamientos"
##
## Duncan's new multiple range test
## for peso
##
## Mean Square Error: 13.34925
##
## tratamientos, means
##
## peso std r Min Max
## trat1 38.610 3.836926 20 33.2 45.6
## trat2 37.355 4.156602 20 32.1 46.7
## trat3 26.600 2.836974 20 21.4 33.2
##
## Alpha: 0.05 ; DF Error: 57
##
## Critical Range
## 2 3
## 2.313628 2.433753
##
## Means with the same letter are not significantly different.
##
## peso groups
## trat1 38.610 a
## trat2 37.355 a
## trat3 26.600 bGraficamos
Como podemos observar en la prueba de comparación de medias entre el tratamiento 1 y 2 no existen diferencias; ambos tratamientos difieren del tratamiento 3, por lo que podemos aplicar cualquiera de los dos normas de riego o sea T1 o T2.
plot(duncan)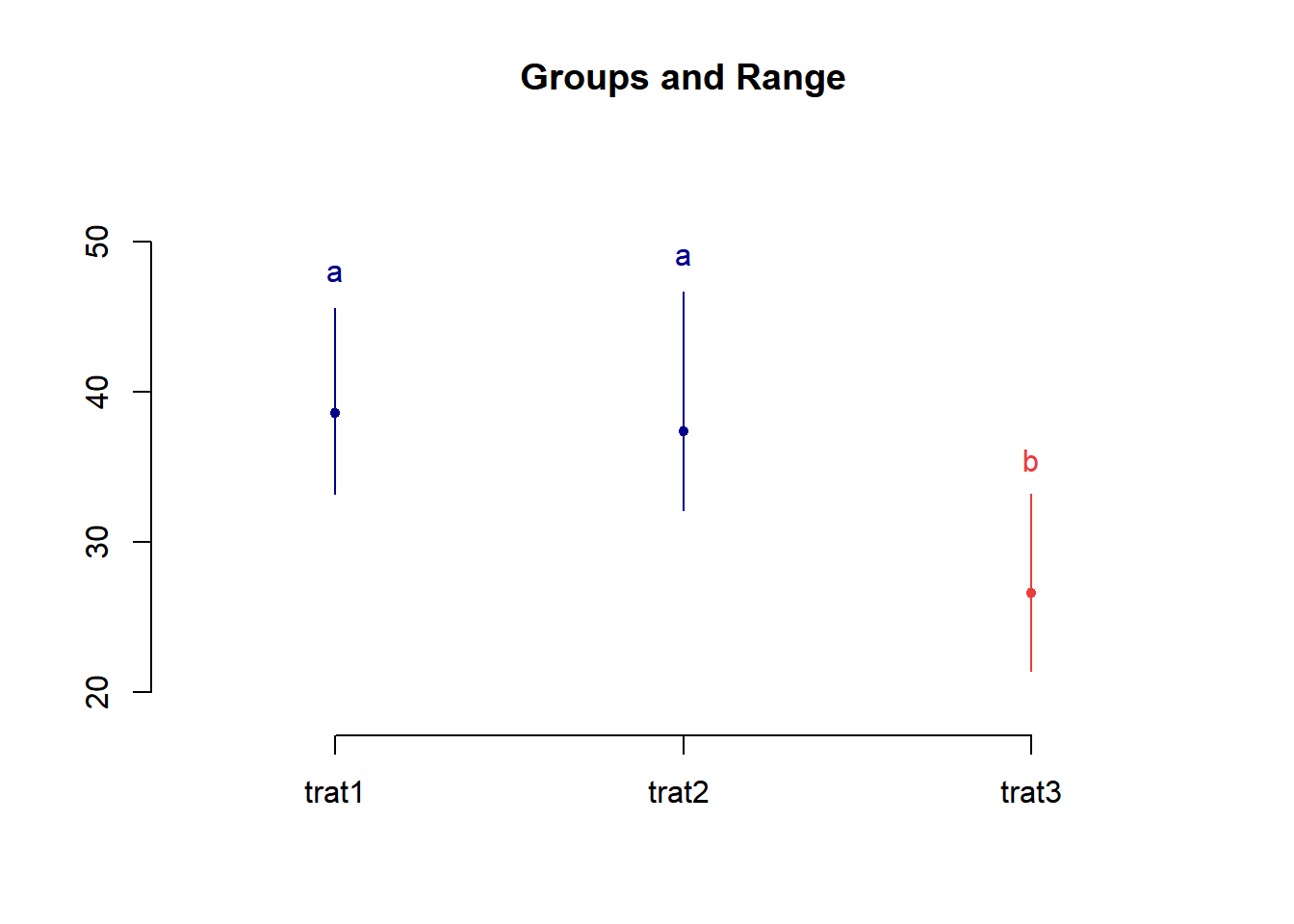
Diseño de bloques al azar
Ejemplo
En un experimento bajo el diseño de bloques al azar se compararon 4 normas de riego en el cultivo del plátano fruta clón “Cavendish gigante”en el ciclo de fomento.
Los tratamientos evaluados fueron:
- T1- Regar cuando la humedad en el suelo llegue a 0,40 bar (40 centibar).
- T2- Regar cuando la humedad en el suelo llegue a 0,45 bar.(45 centibar).
- T3- Regar cuando la humedad en el suelo llegue a 0,5 bar (50 centibar).
- T4- No regar.
Para evaluar los tratamientos se utilizó como variable principal: Rendimiento expresado en toneladas por hectárea, los datos son los siguientes.
## # A tibble: 20 x 3
## tratamientos replicas valor
## <fct> <fct> <dbl>
## 1 A 1 48.0
## 2 A 2 48
## 3 A 3 48.0
## 4 A 4 48.8
## 5 A 5 47.2
## 6 B 1 44.2
## 7 B 2 44.0
## 8 B 3 44.4
## 9 B 4 44.1
## 10 B 5 44.3
## 11 C 1 42.6
## 12 C 2 42.3
## 13 C 3 42.9
## 14 C 4 42.1
## 15 C 5 43.1
## 16 D 1 37.7
## 17 D 2 37.3
## 18 D 3 38.0
## 19 D 4 37.2
## 20 D 5 37Las hipótesis que se van a probar son:
- H0 : T1 = T2 = T3 = T4 vs Al menos un tratamiento desigual.
- H0 : R1 = R2 = R3 = R4 vs Al menos una réplica desigual.
Estas hipótesis se prueban mediante un análisis de varianza.
Realizaremos el análisis del rendimiento expresado en toneladas por hectárea.
modelo <- aov(rendimiento~tratamientos + replicas, data = RBD)
summary(modelo)## Df Sum Sq Mean Sq F value Pr(>F)
## tratamientos 3 287.03 95.68 548.126 4.23e-13 ***
## replicas 4 0.51 0.13 0.729 0.589
## Residuals 12 2.09 0.17
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1En el análisis de varianza podemos observar que para el caso de los 3 tratamientos, en este caso las 4 normas de riego, existen diferencias ya que la Fcal es mayor que la Ftab, con probabilidad de error menor de 0.01. Por lo tanto al menos uno de los tratamientos es diferente a los demás. Para encontrar cuales tratamientos difieren significativamente es necesario hacer una comparación de medias. Entre las réplicas no existen diferencias. Como no sabemos entre cuales tratamientos existen diferencias, debemos aplicar una prueba de comparación de medias.
Comparación de medias por TUKEY
tukey <- HSD.test(modelo,"tratamientos", group=FALSE, alpha = 0.01)
print(tukey)## $statistics
## MSerror Df Mean CV MSD
## 0.17455 12 43.0605 0.9702438 1.027936
##
## $parameters
## test name.t ntr StudentizedRange alpha
## Tukey tratamientos 4 5.501626 0.01
##
## $means
## rendimiento std r Min Max Q25 Q50 Q75
## A 47.990 0.5586591 5 47.20 48.78 47.98 47.99 48.00
## B 44.224 0.1681666 5 44.01 44.45 44.13 44.22 44.31
## C 42.582 0.3898974 5 42.11 43.06 42.30 42.58 42.86
## D 37.446 0.3980955 5 37.00 38.02 37.25 37.30 37.66
##
## $comparison
## difference pvalue signif. LCL UCL
## A - B 3.766 0e+00 *** 2.7380642 4.793936
## A - C 5.408 0e+00 *** 4.3800642 6.435936
## A - D 10.544 0e+00 *** 9.5160642 11.571936
## B - C 1.642 2e-04 *** 0.6140642 2.669936
## B - D 6.778 0e+00 *** 5.7500642 7.805936
## C - D 5.136 0e+00 *** 4.1080642 6.163936
##
## $groups
## NULL
##
## attr(,"class")
## [1] "group"Como podemos observar existen diferencias entre los 4 tratamientos, siendo el de mejor comportamiento regar cuando la humedad del suelo es de 0.40 bar
Graficamos
En este caso usaremos el paquete ggplot2
ggplot(RBD, aes(tratamientos, rendimiento)) +
geom_boxplot(aes(color=rendimiento), show.legend = FALSE) +
theme_bw() +
stat_summary(geom = "point", fun = "mean", color="red")+
xlab("Tratamientos") + ylab("Rendimiento en Kg/ha")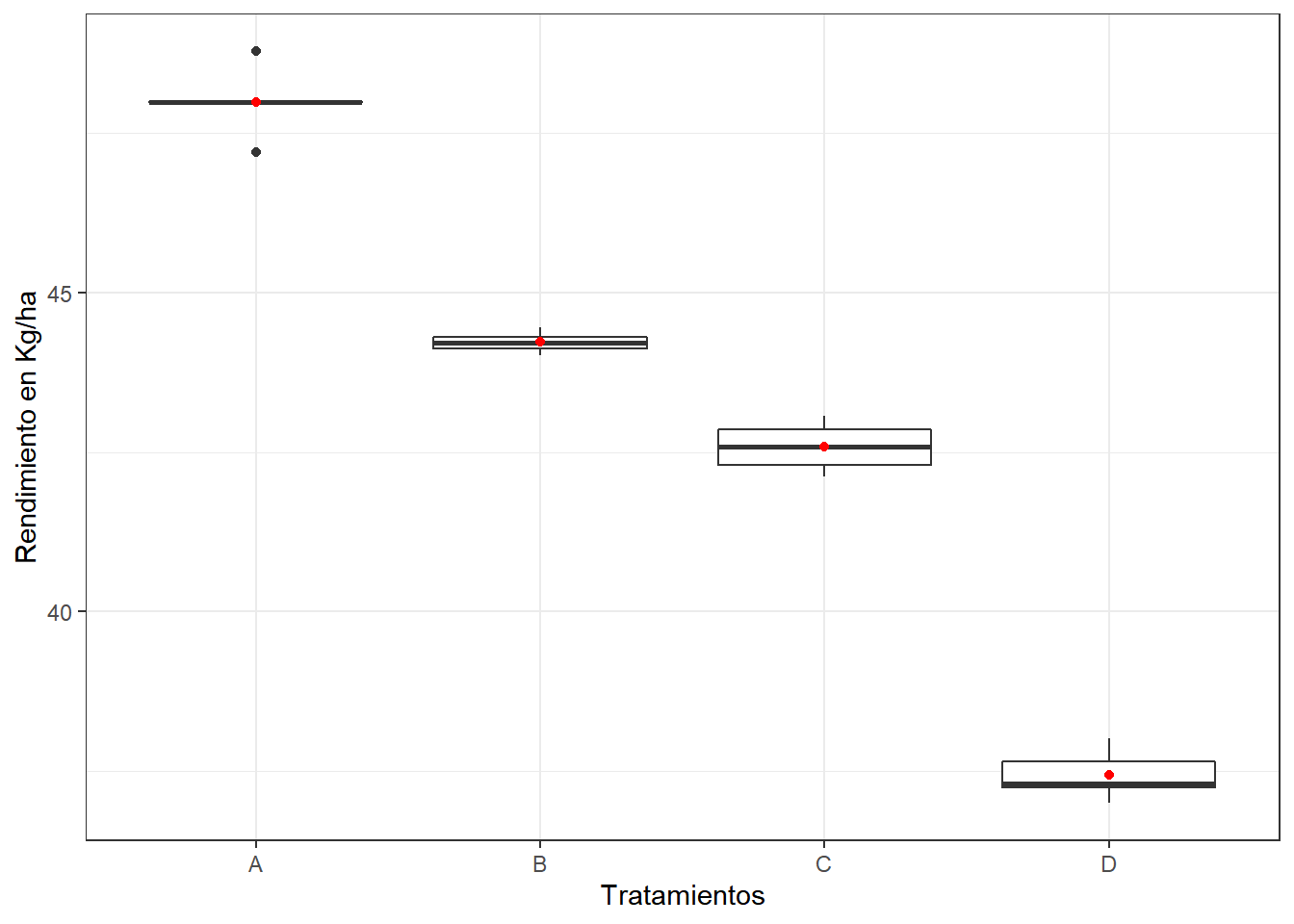 El punto rojo indica la media
El punto rojo indica la media
Contrastes octogonales
Los contrastes ortogonales se utilizan cuando se tienen un conjunto de tratamientos cualitativos con estructura, de tal forma que es conveniente comparar un tratamiento contra el promedio de otros tratamientos o un conjunto de tratamientos contra otro conjunto de tratamientos. Es decir, se prueban hipótesis de la forma:
HO: 3T1 – T2 – T3 – T4 = 0 vs Hl : 3T1 – T2 – T3 – T4 ≠ 0
Esta hipótesis compara el efecto del tratamiento 1 contra el promedio de los efectos de los tratamientos 2, 3, 4.HO: T1 + T2 – T3 – T4 = 0 vs Hl : T1 + T2 – T3 – T4 ≠ 0
Esta hipótesis compara el efecto conjunto del tratamiento 1 y 2 contra el efecto conjunto de los tratamientos 3 y 4.
Ejemplo
Consideremos un experimento donde se compararon 4 variedades de maíz con un diseño de bloques al azar.
- Variedad 1. Precoz resistente.
- Variedad 2. Precoz susceptible.
- Variedad 3. Tardía resistente.
- Variedad 4. Tardía susceptible.
Los datos del rendimiento son:
## # A tibble: 20 x 3
## tratamientos replica rendimiento
## <fct> <fct> <dbl>
## 1 T1 1 6
## 2 T1 2 7
## 3 T1 3 7
## 4 T1 4 8
## 5 T1 5 7
## 6 T2 1 5
## 7 T2 2 6
## 8 T2 3 7
## 9 T2 4 8
## 10 T2 5 8
## 11 T3 1 7
## 12 T3 2 7
## 13 T3 3 8
## 14 T3 4 9
## 15 T3 5 9
## 16 T4 1 8
## 17 T4 2 9
## 18 T4 3 8
## 19 T4 4 10
## 20 T4 5 9Se hace el analisis de varienza igual que en diseño de bloques al azar
modelo <- aov(rendimiento~tratamientos + replica, data = octogonal)
summary(modelo)## Df Sum Sq Mean Sq F value Pr(>F)
## tratamientos 3 12.95 4.317 15.70 0.000187 ***
## replica 4 12.30 3.075 11.18 0.000514 ***
## Residuals 12 3.30 0.275
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Las hipótesis que se desean probar son:
- H0: T1 + T2 – T3 – T4 = 0 vs Hl : T1 + T2 – T3 – T4 ≠ 0
- H0: T1 - T2 = 0 vs Hl : T1 - T2 ≠ 0
- H0: T3 – T4 = 0 vs Hl : T3 – T4 ≠ 0
La primera hipótesis compara las variedades precoces contra tardías la segunda hipótesis compara las dos variedades precoces y la tercera hipótesis compara las dos variedades tardías.
Estas hipótesis se prueban en un análisis de varianza.
Creamos los contrastes
contraste <- rbind(c(1,1,-1,-1),c(1, -1, 0, 0), c(0,0,-1,1))
filas<-c("precoz vs tardio","precoz vs precoz" , "tardia vs tardia")
columnas<-c("V1", "V2","V3", "V4")
dimnames(contraste)<-list(filas,columnas)
dimnames(contraste)## [[1]]
## [1] "precoz vs tardio" "precoz vs precoz" "tardia vs tardia"
##
## [[2]]
## [1] "V1" "V2" "V3" "V4"contraste## V1 V2 V3 V4
## precoz vs tardio 1 1 -1 -1
## precoz vs precoz 1 -1 0 0
## tardia vs tardia 0 0 -1 1Ejecutamos la prueba
con_octo <-glht(modelo, linfct = mcp(tratamientos= contraste))
summary(con_octo)##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Fit: aov(formula = rendimiento ~ tratamientos + replica, data = octogonal)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## precoz vs tardio == 0 -3.0000 0.4690 -6.396 <0.001 ***
## precoz vs precoz == 0 0.2000 0.3317 0.603 0.905
## tardia vs tardia == 0 0.8000 0.3317 2.412 0.091 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)El análisis de varianza muestra que el efecto conjunto de los tratamientos 1 y 2 es diferente al efecto conjunto de los tratamientos 3 y 4. Los tratamientos 1 y 2 no son diferentes. Los tratamientos 3 y 4 difieren significativamente.
Diseño Cuadrado Latino
Ejemplo
En un experimento bajo el diseño de Cuadrado Latino se compararon 5 tipos de fertilizantes:
- F1- NPK + 30 mg bb-16
- F2- NPK + 45 mg bb-16
- F3- NPK + 60 mg bb-16
- F4-NPK.
- F5- Sin fertilizantes.
La tabla siguiente muestra los datos del rendimiento de la soya para los 5 fertilizantes.
Traemos los datos a R en forma Tidy
print(latino[])## # A tibble: 25 x 4
## filas columnas tratamientos rendimiento
## <fct> <fct> <fct> <dbl>
## 1 I 1 F1 22
## 2 I 2 F2 20
## 3 I 3 F3 19
## 4 I 4 F4 10
## 5 I 5 F5 10
## 6 II 1 F2 24
## 7 II 2 F3 17
## 8 II 3 F4 12
## 9 II 4 F5 6
## 10 II 5 F1 21
## # ... with 15 more rowsHacemos eñ analisis de varianza
modelo <- aov(rendimiento~tratamientos+filas+columnas, data = latino)
summary(modelo)## Df Sum Sq Mean Sq F value Pr(>F)
## tratamientos 4 890.8 222.7 44.54 4.18e-07 ***
## filas 4 4.0 1.0 0.20 0.9335
## columnas 4 55.2 13.8 2.76 0.0774 .
## Residuals 12 60.0 5.0
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Para el caso de los tratamientos existen diferencias, por lo que debemos aplicar una prueba de comparación de medias.
DUN <- duncan.test(modelo,"tratamientos", console=TRUE)##
## Study: modelo ~ "tratamientos"
##
## Duncan's new multiple range test
## for rendimiento
##
## Mean Square Error: 5
##
## tratamientos, means
##
## rendimiento std r Min Max
## F1 22.2 1.923538 5 20 25
## F2 22.6 2.073644 5 20 25
## F3 16.4 3.286335 5 11 19
## F4 13.2 2.280351 5 10 16
## F5 6.6 2.408319 5 4 10
##
## Alpha: 0.05 ; DF Error: 12
##
## Critical Range
## 2 3 4 5
## 3.081307 3.225244 3.312453 3.370172
##
## Means with the same letter are not significantly different.
##
## rendimiento groups
## F2 22.6 a
## F1 22.2 a
## F3 16.4 b
## F4 13.2 c
## F5 6.6 dComo podemos observar entre el tratamiento 1 y 2 no existen diferencias, pero si entre estos dos y los restantes.
Experimento bifactorial con diseño completamente al azar
Ejemplo Se realizó un experimento en el cultivo del plátano fruta (Musa AAAB) con el objetivo de evaluar 2 clones con 3 normas riego. Los clones fueron:
-C1 FHIA 01 -C2 FHIA 18
Las normas de riego fueron:
- N1: 25 mm semanales
- N2: 44 mm semanales
- N3: 80 mm semanales
Se muestreó un campo por cada tratamiento midiéndose el peso del racimo (expresado en kg) en 10 m plantones de cada campo.
Los resultados son los siguientes:
Traemos los datos R
## # A tibble: 60 x 3
## clon riego peso
## <fct> <fct> <dbl>
## 1 C1 N1 33
## 2 C1 N1 33.2
## 3 C1 N1 32.9
## 4 C1 N1 33.7
## 5 C1 N1 33.4
## 6 C1 N1 32.6
## 7 C1 N1 34
## 8 C1 N1 33.5
## 9 C1 N1 33.9
## 10 C1 N1 32.9
## # ... with 50 more rowsHacemos el modelo
modelo <- aov(peso~clon*riego, data = bifactorial)
summary(modelo)## Df Sum Sq Mean Sq F value Pr(>F)
## clon 1 318.8 318.8 164.0 < 2e-16 ***
## riego 2 610.6 305.3 157.1 < 2e-16 ***
## clon:riego 2 62.6 31.3 16.1 3.28e-06 ***
## Residuals 54 105.0 1.9
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Se puede observar que para el caso de los tratamientos no buscamos la significación ya que en los experimentos factoriales en los tratamientos están incluidos los factores en estudio y la interacción entre los factores.
Como resultado del análisis de varianza podemos observar que existen diferencias entre la interacción entre los factores clones y normas de riego así como entre los clones y entre las normas de riego. La interpretación de un análisis de varianza de un experimento bifactorial se inicia observando el efecto de la interacción.
En nuestro ejemplo se encontró diferencia significativa en la interacción, por lo que es necesario comparar las medias de la s normas de riego dentro de cada clon y/o las medias de cada clon dentro de cada norma o también comparar todas contra todas.
Hacemos una tabla de promedios
model.tables(modelo, "mean")## Tables of means
## Grand mean
##
## 32.57167
##
## clon
## clon
## C1 C2
## 30.27 34.88
##
## riego
## riego
## N1 N2 N3
## 36.73 28.98 31.99
##
## clon:riego
## riego
## clon N1 N2 N3
## C1 33.31 26.45 31.04
## C2 40.16 31.52 32.95Evaluamos las interacciones
posthoc <- lsmeans(modelo,
pairwise ~ clon*riego,
adjust="tukey")
cld(posthoc[[1]],
alpha=.05,
Letters=letters)## clon riego lsmean SE df lower.CL upper.CL .group
## C1 N2 26.4 0.441 54 25.2 27.7 a
## C1 N3 31.0 0.441 54 29.8 32.2 b
## C2 N2 31.5 0.441 54 30.3 32.7 bc
## C2 N3 33.0 0.441 54 31.7 34.2 c
## C1 N1 33.3 0.441 54 32.1 34.5 c
## C2 N1 40.2 0.441 54 39.0 41.4 d
##
## Confidence level used: 0.95
## Conf-level adjustment: sidak method for 6 estimates
## P value adjustment: tukey method for comparing a family of 6 estimates
## significance level used: alpha = 0.05Medias con letras diferentes difieren significativamente, P < 0.05 Como podemos observar existen diferencias entre la combinación C2N1 con el resto de las combinaciones, no existen diferencias entre C1N1 y C2N3, ni entre C2N2 y C1N3, así como entre A1B2 y el resto de las combinaciones resultando la mejor combinación A2B1 y la peor C1N2.
Graficamos la interacción
plot <- ggline(bifactorial, x = "riego", y = "peso", color = "clon",
add = c("mean_se", "dotplot")) +theme_bw() + ggtitle("Grafica de interaccion")
plot## `stat_bindot()` using `bins = 30`. Pick better value with `binwidth`.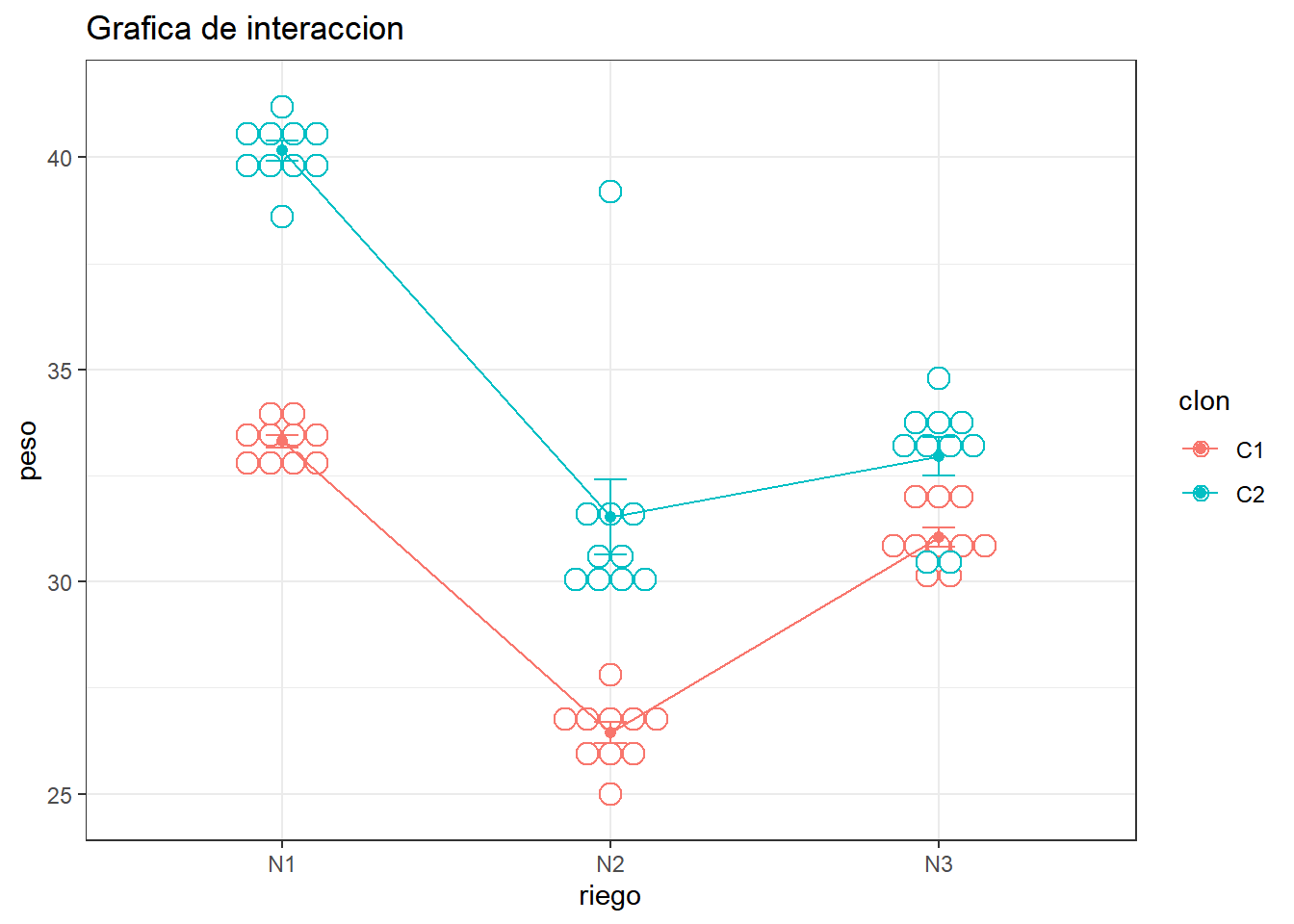
Bibliografia
Universidad Jose Carlos Mariategui. Experimentacion agricola. Escuela Profesional de ingenieria agronomica. Peru. 2009